CSGA member Lamont Anderson penned the following observations about Ed Strecker's idea to incorporate some features of Napoleon's Battles (NB) into Commands & Colors Napoleonics (CCN). Below are Lamont's thoughts on Ed's idea:
So... many of you saw Ed and I pushing 28s in a Commands & Colors Napoleonics first game awhile ago. Ed is generating a mash-up of CCN with NB that adds a little "NB chrome" without insulting the simple game mechanism in CCN.
As an example, Ed has this cool idea for using the NB response numbers to good purpose in CCN. Range of response in NB is 4 (Russian line) to 8 (French Old Guard), and Ed's first cool idea is to add to CNN a response roll to make square against cav: roll your response # in 6-sided dice and get > or equal Infantry symbols (2 per die) over cav symbols (1 per die).
So like none of you has ever tried to figure dice odds either, right? ;-)
So if you are interested read on.. (Below are the Excel spread sheet tables.)
In order to evaluate such game mechanics, we needed a table of percentages for dice outcomes. If I roll 8 dice in a FrOGD response, what chance 3 of them are infantry. And if that occurs, what chances are cavalry gonna show on the remaining five dice?
Well. I wrestled with this much of today, and I stumbled on Pascal's Triangle: https://en.wikipedia.org/wiki/Pascal%27s_triangle
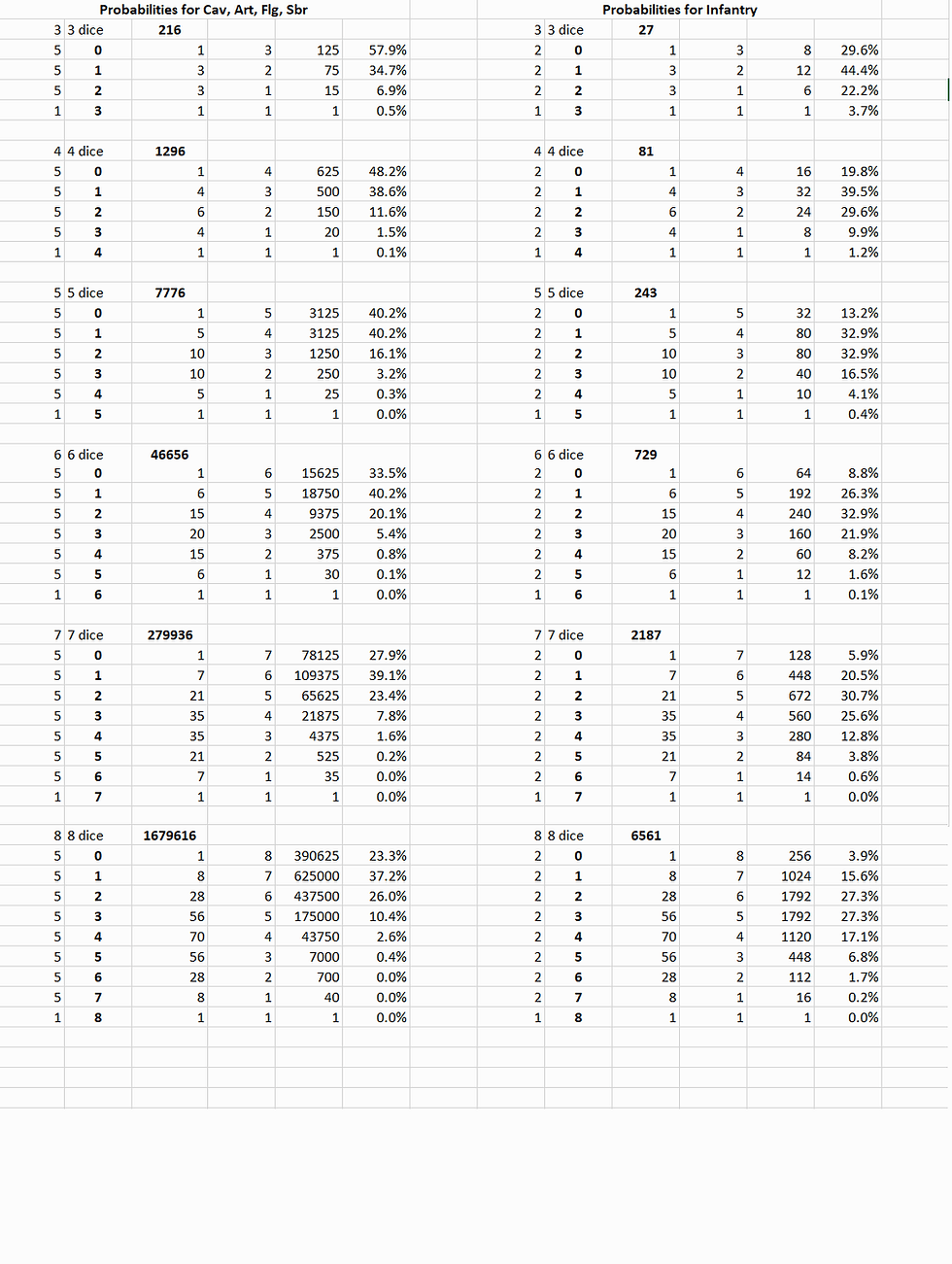
It can do many things, one of which is tell you how many different ways a set number of dice can give a desired result (like you can make 7 six different ways on 2 x D6). It works like this: If you wanna know how many ways 6 dice can produce unique sets of 3 sixes, go to 6th row of the triangle, then right 3 columns. You can see my Pascal coefficients in the second sheet called "data" if you wish. Under the "6 dice" section, the Pascal coefficient of "15" means there are 15 different ways I can get 3 sixes out of 6 x D6. I just thought that was cool.
So the two tables (shown below) present % for infantry outcomes (they get two faces on the D6) vs dice #, as well as same for "other" meaning any other single symbol (Cav, Arty, Flag, Saber). We might try these tables in evaluating Ed's idea on response rolls for making square (see above).
FrOGD: will roll 4 or more INF ~25% of the time on 8 dice, which means auto-square, (CAV cannot be more than 4 here) But then, % chance of rolling 3 x INF = 27.3% (see first table) If 3 of 8 dice are INF, that leaves 5 that can roll up as cavalry, which moves it to the 5-dice column of the second table % chance of rolling 4 x CAV on five dice is 0.3%
What about FrOGD rolling up only 2 x INF? there is also a 27.3% of that happening with 8 dice, leaving 6 dice that can roll up 3 or more Cav at ~6.3%.
Now the FrOGD do have a 15.6% chance of rolling only 1 x INF in 8 dice, leaving 7 dice that have 33% of hitting 2 or more CAV
Finally, what if 8 dice yield NO INF- there is 3.6% chance of that, and then 8 dice could cause square failure at ~76% of the time with 1 or more CAV
I do not even know if this is appropriate use of the percentages in these tables (I am very weak on statistics).
But then....
How about Russian line infantry with response 4? With only four dice, Russian line will auto-square on 2-4 INF, which they will do ~40% of the time. RsLN will roll 1 x INF 39.5% of the time, leaving three dice to make 2 or more CAV at 7.4%; RsLN will roll NO INF 19.8% of the time, leaving 4 dice to roll 1 or more CAV at ~52%, failing square.
These two comparisons in the extreme suggest to me that Ed's idea on NB response values is diceable in this game system!
- Lamont
Table 1
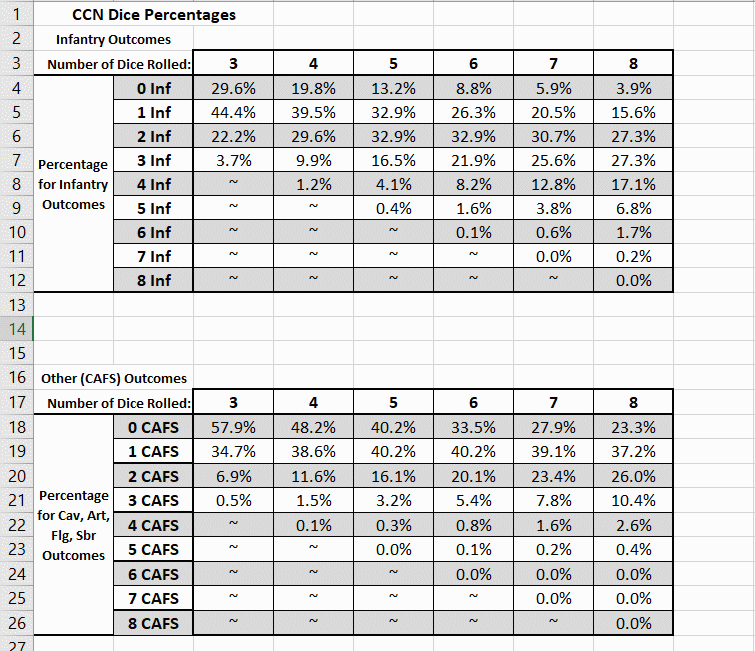
Table 2
